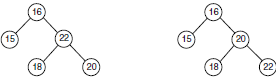
À la fin de cette séquence vous serez capable de :
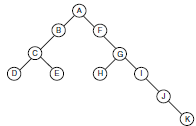
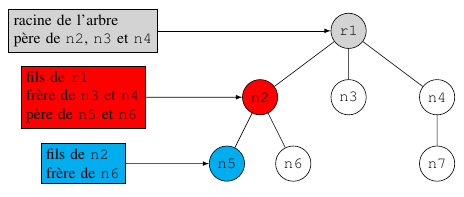
Un arbre est une structure de données similaire à une liste chaînée, mais au lieu que chaque nœud pointe simplement vers le nœud suivant de manière linéaire, chaque nœud pointe vers plusieurs nœuds. Un arbre est un exemple de structure de données non linéaire. La structure est une façon de représenter la nature hiérarchique d'une structure sous une forme graphique.


Un arbre est appelé arbre binaire si chaque nœud a zéro enfant, un enfant ou deux enfants.
L'arbre vide est également un arbre binaire valide.
Un nœud n'ayant aucun fils est appelé feuille ou nœud externe.
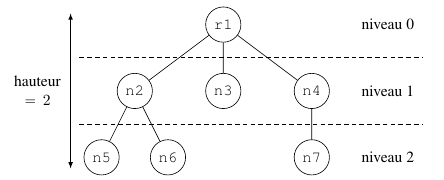
La profondeur d’un nœud est la longueur du chemin simple entre la racine et ce noeud.
Un niveau c'est l’ensemble de tous les nœuds de même profondeur.
La hauteur d'un arbre ou profondeur d'un arbre est le nombre total de niveaux de l'arbre.
La taille d'un arbre est le nombre de noeuds de cet arbre.
Un arbre binaire peut également être défini comme une structure récursive. Ainsi, un arbre binaire AB est soit vide soit se compose de :
Quelques opérations auxilliaires
Afin de traiter les arbres, on a besoin de visiter ses différents nœuds.
Le processus de visite de tous les nœuds d'un arbre est appelé parcours d'arbre. Chaque nœud n'est traité qu'une seule fois mais il peut être visité plus d'une fois.
Le parcours s'effectue comme suit :
L'algorithme du parcours préfixe
Fonction parcours_prefixe(AB)
"""
Entrée : AB est un arbre binaire ;
Sortie : Tous les noeuds de l'arbre ont été visités en préfixe.
"""
Si AB n'est pas vide,
renvoyer la cle de la racine de AB cas de base
parcours_prefixe(sous-arbre gauche de AB)
parcours_prefixe(sous-arbre droit de AB)
FinSi
FinFonction
Exemple :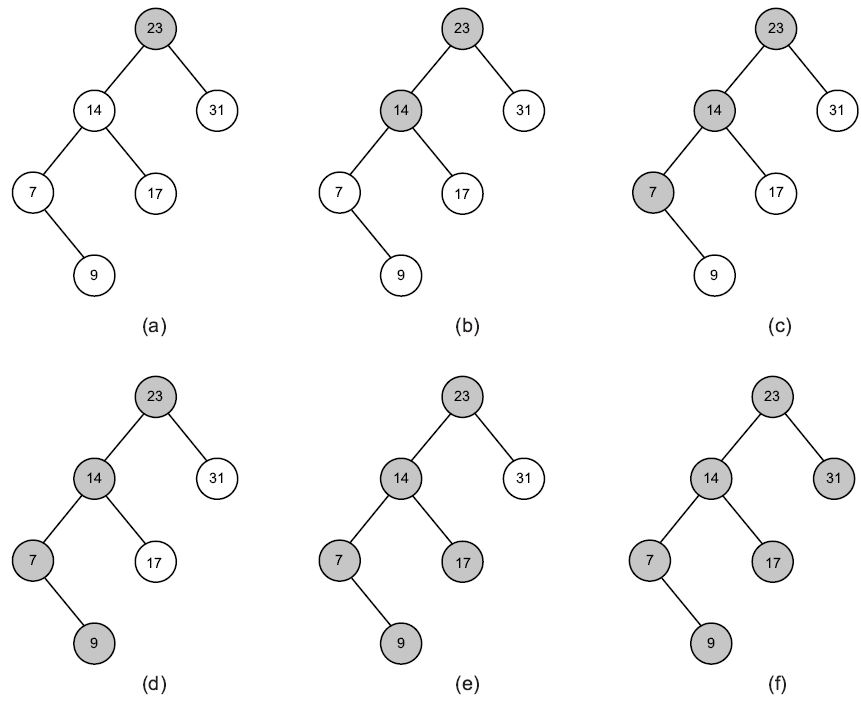
Le parcours s'effectue comme suit :
Exemple :
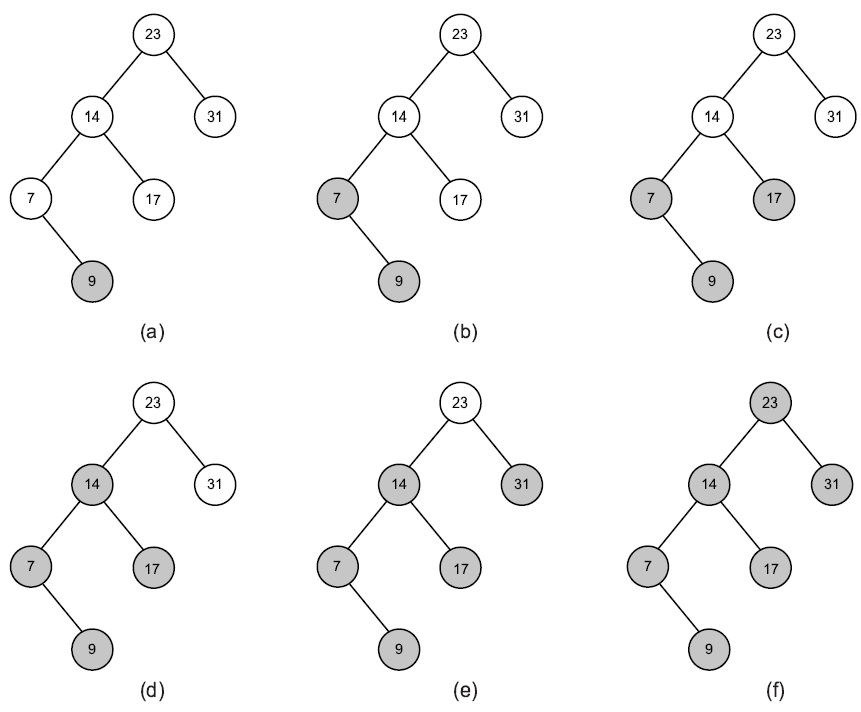
Le parcours s'effectue comme suit :
L'algorithme du parcours
Fonction parcours_infixe(AB)
"""
Entrée : AB est un arbre binaire ;
Sortie : Tous les noeuds de AB ont été visités en infixe.
"""
Si AB n'est pas vide,
parcours_infixe(sous-arbre gauche de AB)
renvoyer la clé de la racine de AB
parcours_infixe(sous-arbre droit de AB)
FinSi
FinFonction
Exemple :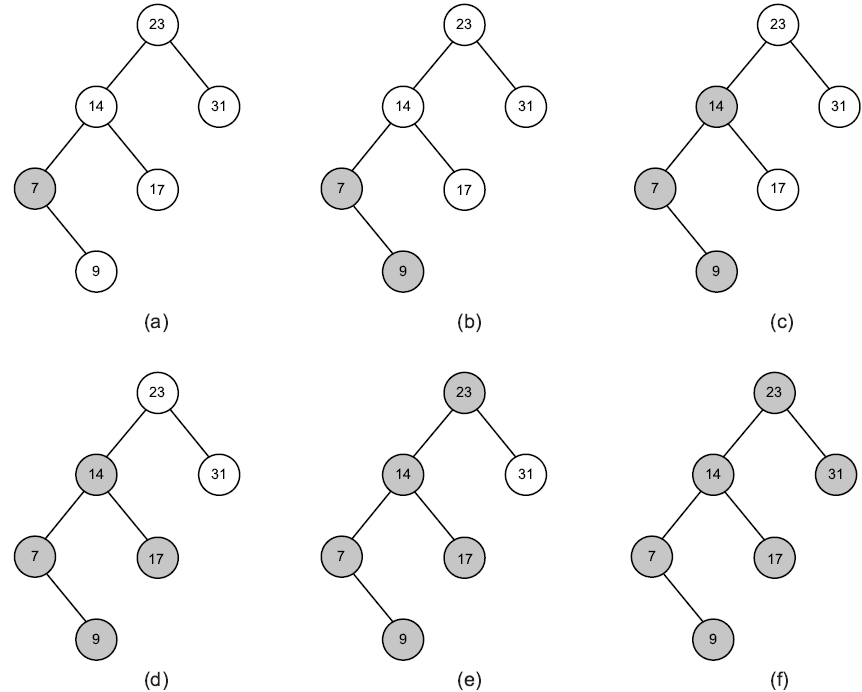
Parcourir un arbre en largeur d'abord revient à parcourir un arbre niveau par niveau. On visite la racine, puis tous les noeuds de niveau 1, en partant de la gauche vers la droite, puis tous les noeuds de niveau 2. Ainsi de suite.
L'algorithme du parcours
Traditionnellement, le parcours en largeur d'abord est implémenté en utilisant une liste pour stocker les valeurs des nœuds visités dans le parcours en largeur d'abord, puis une file d'attente pour stocker les nœuds qui n'ont pas encore été visités.
Fonction parcours_en_largeur(AB)
"""
Entrée : AB est un arbre binaire ;
Sortie : Tous les noeuds de AB ont été visités en largeur d'abord.
"""
F est une file vide
lst est une liste vide
Tant Que AB n'est pas vide :
insérer la clé de la racine de AB dans lst
Si le sous-arbre gauche de AB n'est pas vide,
enfiler dans F le sous-arbre gauche de AB
FinSi
Si le sous-arbre droit de AB n'est pas vide,
enfiler dans F le sous-arbre droit de AB
FinSi
Si F n'est pas vide,
racine ← défiler(F)
Sinon:
racine ← None
FinSi
Fin Tant que
FinFonction
Exemple :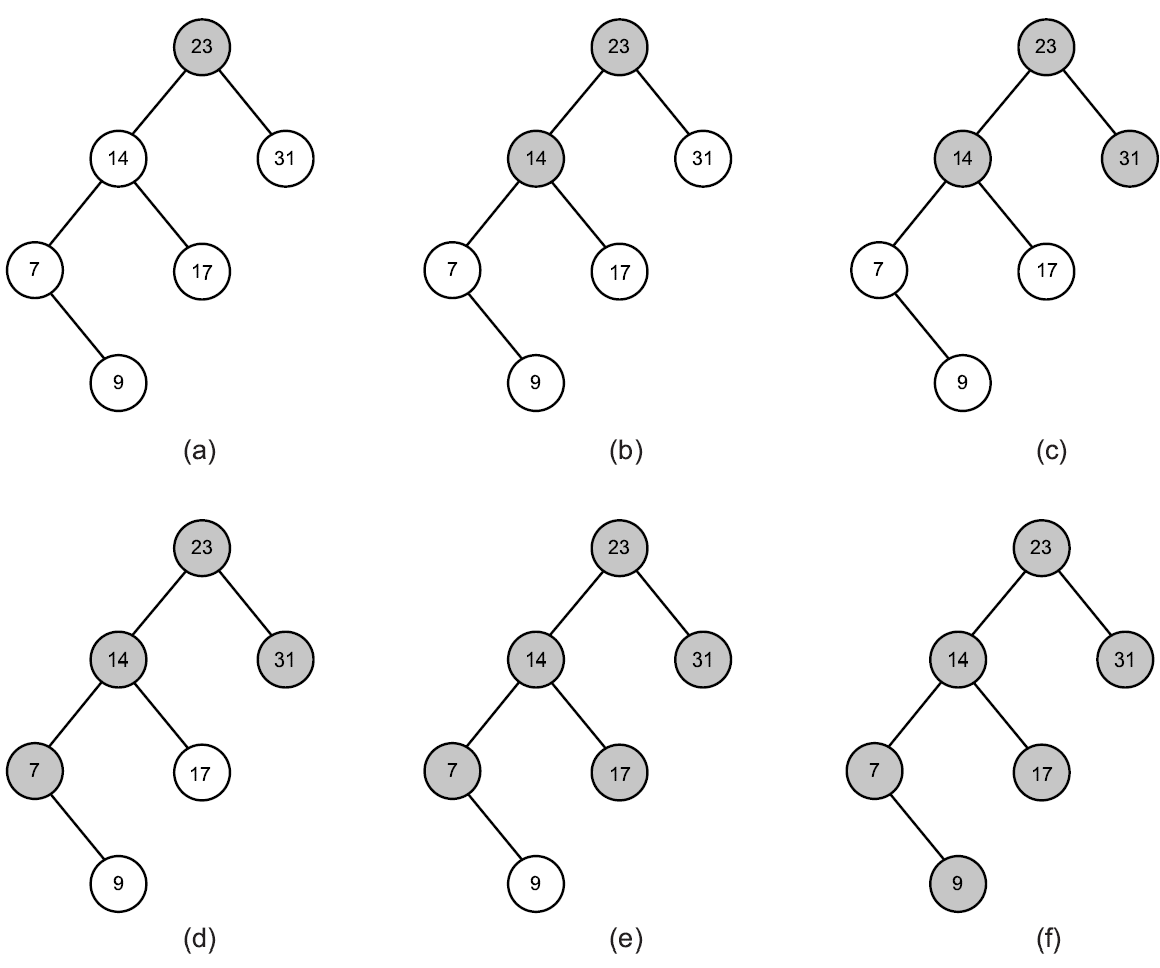
Calculez la taille des sous-arbres gauche et droit de manière récursive, ajoutez 1 (nœud racine).
L'algorithme de détermination de la taille
Fonction taille_recursive(AB):
"""
Entrée : AB est un arbre binaire ;
Sortie : Renvoie le nombre de clé de l'AB.
"""
Si AB est vide :
renvoyer 0
sinon:
renvoyer taille_recursive(sous-arbre gauche de AB) + taille_recursive(sous-arbre droit de AB) + 1
FinSi
FinFonction
class Noeud:
"""Modélise un nœud d'un arbre binaire."""
def __init__(self, cle, gauche = None, droit = None):
self.cle = cle
self.gauche = gauche
self.droit = droit
#Afficher le noeud
def __str__(self):
"""Affiche la valeur (cle) du nœud."""
return f"{self.cle}"
def __repr__(self):
"""Affiche le nœud."""
return f"Noeud({repr(self.cle)}, {repr(self.gauche)}, {repr(self.droit)})"
class ArbreBinaire:
"""Représente un arbre binaire."""
def __init__(self, racine):
self.racine = racine
#Afficher l'AB
def __repr__(self):
"""Affiche l'arbre binaire."""
return f"ArbreBinaire({repr(self.racine)})"
def est_vide(self):
"""Renvoie True si l'AB est vide, False sinon."""
return self.racine is None
def get_droit(self):
"""Renvoie l'AB droit."""
def get_gauche(self):
"""Renvoie l'AB droit."""


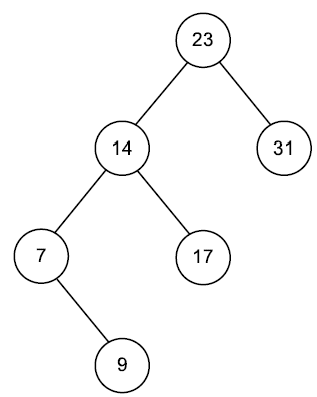
noeud7 = Noeud(7)
noeud9 = Noeud(9)
noeud14 = Noeud(14)
noeud17 = Noeud(17)
noeud23 = Noeud(23)
noeud31 = Noeud(31)
noeud23.gauche = noeud14
noeud23.droit = noeud31
noeud14.gauche = noeud7
noeud14.droit = noeud17
noeud7.droit = noeud9
mon_AB = ArbreBinaire(noeud23) #un arbre est identifié par sa racine
# Une autre façon de représenter le noeud14
exple = Noeud(14, gauche=noeud7, droit=noeud17)
repr(exple)
#un noeud est considéré comme un arbre binaire
class AB:
"""Représente un arbre binaire."""
def __init__(self, cle, gauche = None, droit = None):
self.cle = cle
self.gauche = gauche
self.droit = droit
#Afficher l'arbre
def __repr__(self):
"""Affiche l'AB."""
return f"AB({repr(self.cle)}, {repr(self.gauche)}, {repr(self.droit)})"
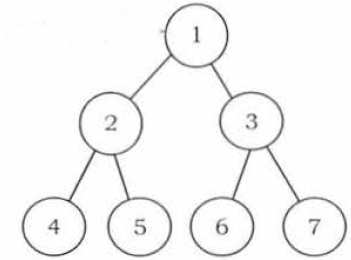
# une instance de cet arbre
gauche = AB(2)
droit = AB(3)
arbre = AB(1, gauche, droit)
#de façon plus concise
arbre = AB(1, AB(2), AB(3))
Écrire puis l'insérer dans la classe AB la fonction d'arbre binaire ajoute_a_gauche(AB, donnee) qui insère la clé donnee comme clé du sous-arbre gauche de AB.
Une expression est une suite de symboles qui suivent des règles données. Un symbole peut être soit un opérande, soit un opérateur. On considère, ici, uniquement les opérateurs arithmétiques binaires sous la forme opérande-opérateur-opérande. Les opérateurs arithmétiques standard sont +, -, × et /.
Un arbre d'expression est un arbre binaire avec les propriétés suivantes :
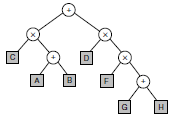
Exemple : a × (b + c) + d

Il s'agit d'arbres binaires étiquetés aux sommets. L'étiquette d'un sommet est la clé ou le contenu du sommet.
Contrairement à un arbre binaire général, les clés d’un ABR doivent être comparables entre elles.
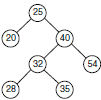
Ainsi, un ABR a les propriétés suivantes :

L'algorithme de recherche de la plus grande clé dans l'ABR
maximum_recursive(ABR)
"""
Entrée : ABR est un arbre binaire de recherche ;
Sortie : La clé la plus grande dans l'ABR.
"""
Si l'ABR droit est vide,
renvoyer la clé de la racine cas de base
Sinon
maximum_recursive(ABR.droit) cas récursif
FinSi
FinFonction
Écrire l'algorithme de recherche de la plus petite clé dans l'ABR, minimum_recursive(ABR).
L'algorithme de la fonction recherche_recursive
Fonction recherche_recursive(ABR, donnee)
"""
Entrée : ABR est un arbre binaire de recherche ;
donnee est une valeur.
Sortie : True si donnee appartient à l'ABR, False sinon.
"""
Si ABR est vide,
renvoyer False cas de base
FinSi
Si donnee < clé de la racine,
renvoyer recherche_recursive(ABR_gauche, donnee)
Sinon
Si donnee > clé de la racine,
renvoyer recherche_recursive(ABR_droit, donnee)
Sinon #donnee = clé de la racine
renvoyer True cas de base
FinSi
FinSi
FinFonction
Écrire l'algorithme de la fonction insere_recursive(ABR, donnee)
class Noeud:
"""Modélise un noeud d'un arbre binaire de recherche."""
def __init__(self, cle, gauche = None, droit = None):
self.cle = cle
self.gauche = gauche
self.droit = droit
#Afficher le noeud
def __str__(self):
"""Affiche la valeur (cle) du noeud."""
return f"{self.cle}"
def __repr__(self):
"""Affiche le noeud."""
return f"Noeud({repr(self.cle)}, {repr(self.gauche)}, {repr(self.droit)})"
class ABR:
"""Représente un arbre binaire de recherche."""
def __init__(self, racine):
self.racine = racine
#Afficher l'ABR
def __repr__(self):
"""Affiche l'ABR."""
return f"ABR({repr(self.racine)})"
def est_vide(self):
"""Renvoie True si l'ABR est vide, False sinon."""
return self is None